Solution: An acrobat has a weight of 150 lb and is sitting on a chair which is perched on top of a pole as shown. If by a mechanical drive the pole rotates downward at a constant rate from theta=0 degrees, such that the acrobat's center of mass G maintains a constant speed of v(a)=10 ft/s, determine the angle theta at which he begins to fly out of the chair. Neglect friction and assume that the distance from one pivot O to G is 15 ft.

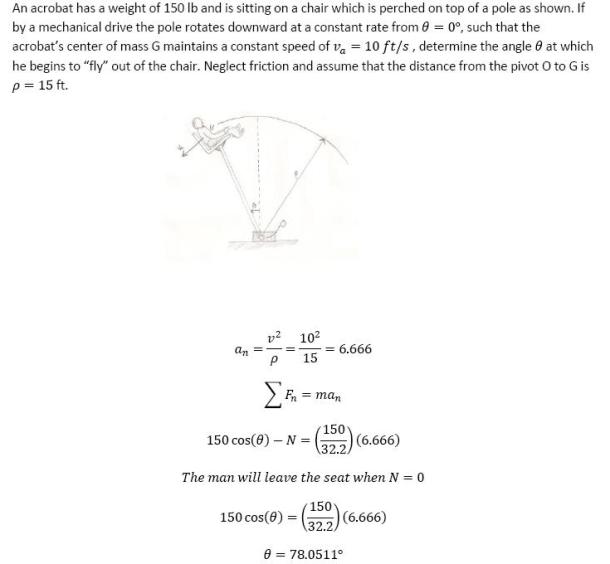
dynamics math problems engineering equations dynamics basic mechanics school homework engineering math dynamics formulas dynamics problems dynamics problem solutions to dynamics problems full solution dynamics engineering dynamics problem solution dynamics math problems engineering equations dynamics basic mechanics school homework engineering math dynamics formulas dynamics problems dynamics problem solutions to dynamics problems full solution dynamics engineering dynamics problem solution

Highalphabet Home Page dynamics problem solution dynamics math Highalphabet Statics Lessons

An acrobat has a weight of 150 lb and is sitting on a chair which is perched on top of a pole as shown. If by a mechanical drive the pole rotates downward at a constant rate from theta=0 degrees, such that the acrobat's center of mass G maintains a constant speed of v(a)=10 ft/s, determine the angle theta at which he begins to fly out of the chair. Neglect friction and assume that the distance from one pivot O to G is 15 ft.