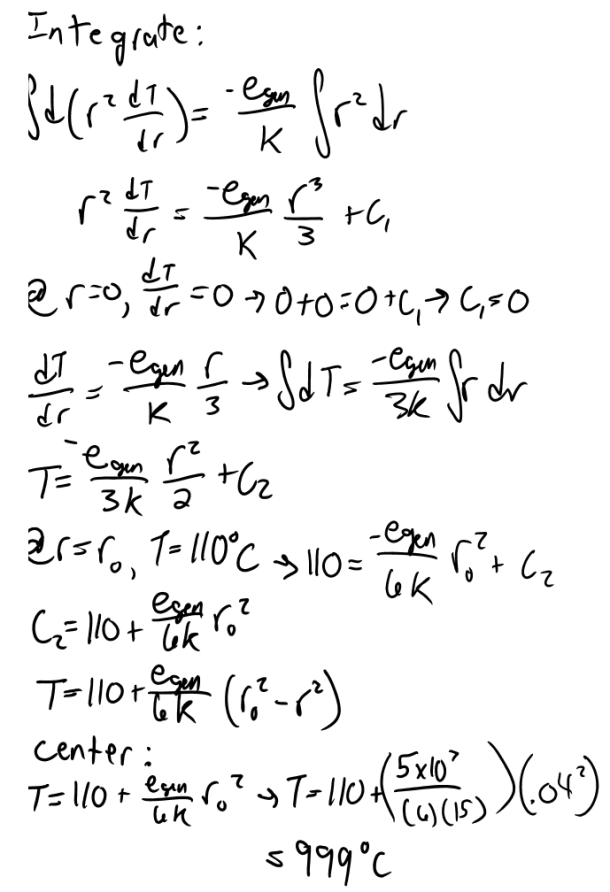heat and mass transfer problems engineering equations heat and mass transfer school homework engineering heat and mass transfer formulas heat and mass transfer solutions to heat and mass transfer problems full solution engineering problem solution heat and mass transfer math problems engineering equations heat and mass transfer school homework engineering solutions to heat and mass transfer formulas heat problems mass problem solutions to transfer problems full solution heat and mass transfer

heat and mass transfer problems engineering equations heat and mass transfer school homework engineering heat and mass transfer formulas heat and mass transfer solutions to heat and mass transfer problems full solution engineering problem solution heat and mass transfer math problems engineering equations heat and mass transfer school homework engineering solutions to heat and mass transfer formulas heat problems mass problem solutions to transfer problems full solution heat and mass transfer

Highalphabet Home Page heat and mass transfer solutions Heat and Mass Transfer Page

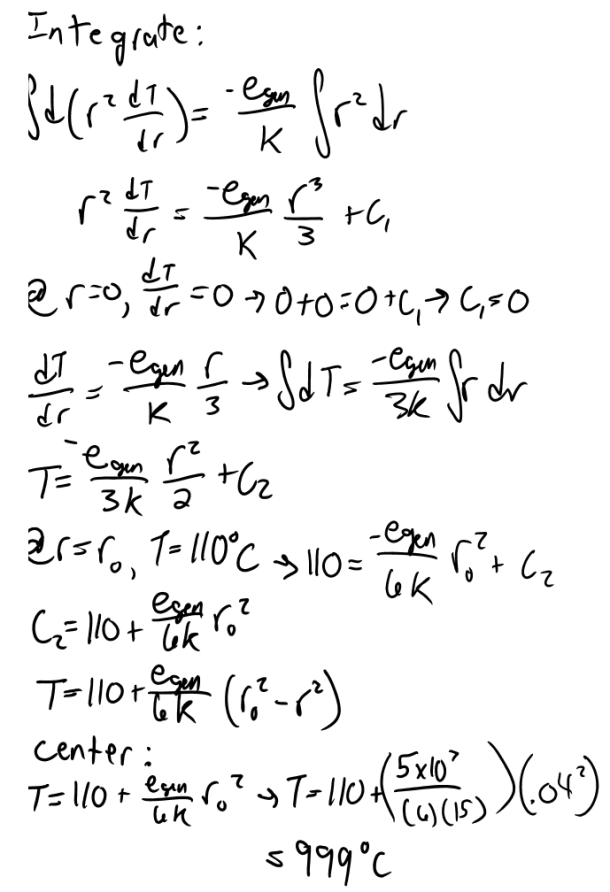
Consider a homogenous spherical piece of radioactive material of radius r0=0.04 m that is generating heat at a constant rate of 5x10^7 W/m^3. The heat generated is dissipated to the environment steadily. The outer surface of the sphere is maintained at a uniform temperature of 110 C and the thermal conductivity of the sphere is k= 15 W/mK. Assuming steady one dimensional heat transfer, (a) express the differential equation and the boundary conditions for heat conduction through the sphere, (b) obtain a relation for the variation of temperature in the sphere by solving the differential equation, and (c) determine the temperature at the center of the sphere.