heat and mass transfer problems engineering equations heat and mass transfer school homework engineering heat and mass transfer formulas heat and mass transfer solutions to heat and mass transfer problems full solution engineering problem solution heat and mass transfer math problems engineering equations heat and mass transfer school homework engineering solutions to heat and mass transfer formulas heat problems mass problem solutions to transfer problems full solution heat and mass transfer

heat and mass transfer problems engineering equations heat and mass transfer school homework engineering heat and mass transfer formulas heat and mass transfer solutions to heat and mass transfer problems full solution engineering problem solution heat and mass transfer math problems engineering equations heat and mass transfer school homework engineering solutions to heat and mass transfer formulas heat problems mass problem solutions to transfer problems full solution heat and mass transfer

Highalphabet Home Page heat and mass transfer problem solutions Heat and Mass Transfer Page

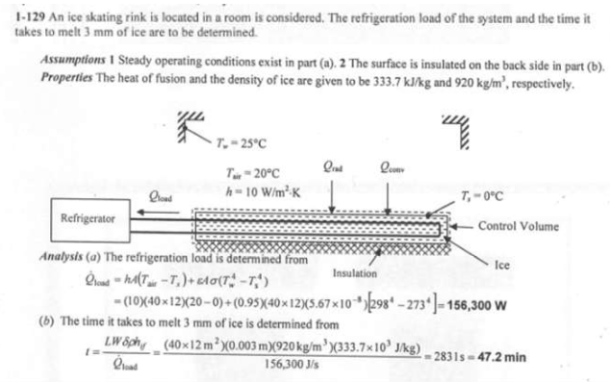
An ice skating rink is located in a building where the air is at T_air=20 C and the walls are at T_w=25 C. The convection heat transfer coefficient between the ice and the surrounding air is h=10 W/m^2K. The emissivity of ice is 0.95. The latent heat of fusion of ice is 333.7 kJ/kg and its density is 920 kg/m^3. (a) Calculate the refrigeration load of the system necessary to maintain the ice at T_s=0 C for an ice rink of 12 m by 40 m. (b) How long would it take to melt 3 mm of ice from the surface of the rink if no cooling is supplied and the surface is considered insulated on the back side?